プラントを設計するにあたり、計装関連を任されたときに、意外と重要なポイントが各計装機器の許容誤差をどの程度にするのか決める事です。もちろんすべて、高精度の機器を取りそろえるのが理想ですが、価格も高いので、特に精度が求められない場所については、安価な計器にするべきです。
また、上手くいくか分からない新規の製造プラントなどにおいて、実際出来上がって運転したときに上手く製品ができない事があります。なので、前もって各計器の精度について取り決めておいて、それを達成すればOKというような検収条件にすることで、プラントを実働させたときに上手く製品が出来なかった時の保険にできます。
そこで、計器の精度について、設計の段階でどのくらいズレそうかある程度根拠を持って、話ができるよう総合誤差について記します。
・注意
以降の誤差に関する内容は、私個人の認識によるもので、学問的に正しいかどうかわかりません。特に確率統計を専門にしている方には、正当を教えてもらいたいです。計装の誤差について取り扱っておいて何ですが、適当でよいと思ってます。肝心なのは、相手がどんな製品を製造したいか、要求する仕様を満たす事です。「誤差についてきちんと気にしてますよ」という雰囲気を出すのが重要で、相手が納得してくれればいいわけです。そのための「総合誤差についてはこういう風に計算します。これをもとに、試運転で許容できる範囲内か判断します。」という判断材料になればと思います。
総合誤差の扱い方について
・総合誤差
JIS規格では、総合誤差について以下のように定義しています。
種々の要因によって生じる誤差のすべてを含めた総合的な誤差。
JIS Z 8103 計測用語 より
総合誤差についての計算のしかたについては、JISには記載がありません。「種々の要因によって生じる誤差」とは、計装でいうところの「アナログ検出器、変換器、演算器、調節計」などにあたります。そして、これらの誤差をすべて含めた総合的な誤差の計算方法は、下記の3つがあります。
- 2乗平均誤差(MSE)
- 2乗平均の平方根(RMS)
- 2乗和平方根(SRSS)
ちなみに、私が学校で教わったのは、2乗平均誤差です。しかし、会社で教わったのは、2乗和平方根の計算でした。
分かりやすいモデル

分かりやすい総合誤差はなんだろうと考えた時に、一番悪いパターンで測定値を読み取った場合が当てはまると思います。上の図のように、本来はありえませんが、流量計とA/D変換器がどちらも、分かりやすいように誤差をF.S.±10%としています。これらは、フルスケール精度と表現します。
上の図のようにワーストケースで誤差の伝搬について考えると、最終的にデジタル変換して表示される測定値の誤差が±40%になります。しかし、確立と統計について知っている方はこれが正しくない事を知っています。読み値が「真値±誤差」の範囲にだいたい68%ぐらいの確率で入ってる時の範囲を誤差として扱ってると思います。
・計器の各用語について
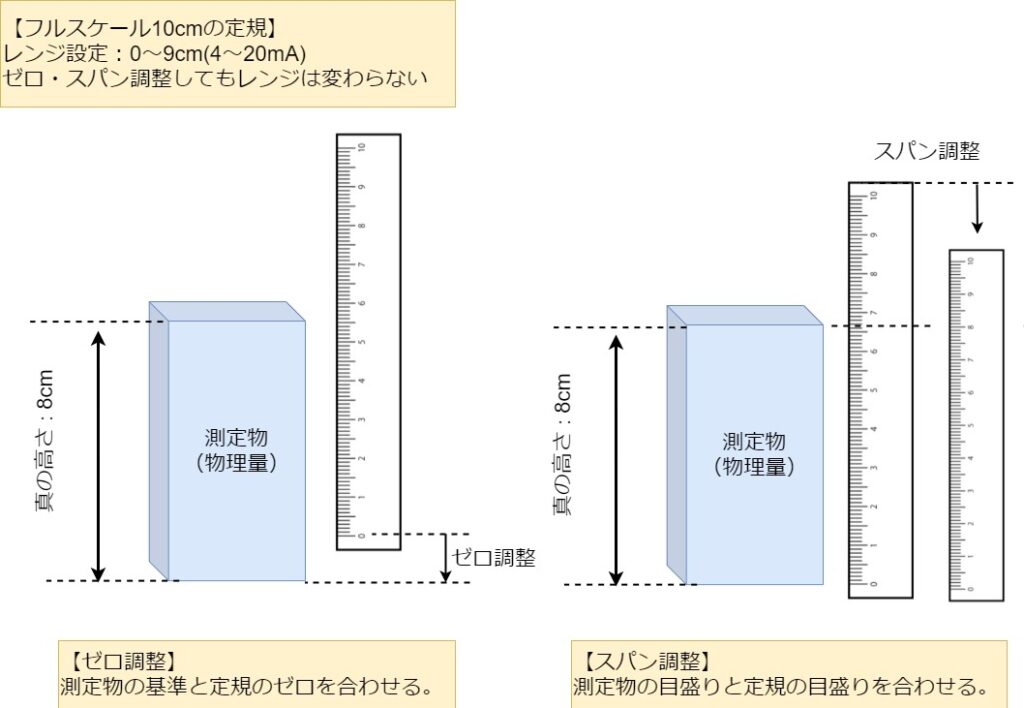
巻き尺や定規に測定できる上限があるように計器にも定格(保証できる測定限度)が存在します。ちなみに4~20mAを0~100L/minと設定することをレンジ設定といいます。また、計器を取り付けても、ちゃんと測定できているかの保証はできません。大きさや流量、温度など物理量を圧電素子やホール素子などのアナログ信号に変える所で誤差があるかもしれません。つまり、物理量の変化に対するアナログ信号の間隔、スパン誤差です。イメージとしては、定規の1cm間隔があってないという感覚です。製造メーカーは製品検査をしますが、実現場と環境が違います。そのため、実際に現地にて試運転を行い、「今この状態をゼロとし4mAを出力させる」、「今この状態を信号レベル50%とし、12mAを出力させる」、「今この状態を信号レベル100%とし、20mAを出力させる」、「今の状態を、この値として認識し、電流出力してくださいと、計器に書き込む」など、計器の内部検出値に対して倍率(比例の傾き)の調整を行う事をゼロ・スパン調整と表現したりします。ゼロ・スパン調整をしても設定したレンジは変わりません。フルスケールの誤差の場合、信号レベル50%のときは、単純に誤差が2倍になりますので、測定スパンを広く設定し、低い信号レベルで扱うと、誤差が多くなりますので注意してください。
2乗平均誤差(MSE)
誤差といえば、標準偏差のことをですが、標準偏差の平方根をとらない形を2乗平均誤差といいます。nを誤差要因になる機器の数、xiを測定値、Sを真の値とすると下記の式になります。
$$MSE=\frac{1}{n}\sum_{i=1}^{n}{(x_{i}-S)^{2}}$$
私の持っている参考書には、アナログ方式の総合誤差は、2乗平均誤差で求めると記載ありますが、なんか違う感じがします。
2乗平均の平方根(RMS)
2乗平均の平方根は、お馴染みの標準偏差です。上記で述べた、「わかりやすいモデル」で扱った、流量計やアナログ入力カードの誤差は、標準偏差で表されていると考えるとしっくりきます。 nを誤差要因になる機器の数、xiを測定値、Sを真の値とすると下記の式になります。
$$RMS=\sqrt{\frac{1}{n}\sum_{i=1}^{n}{(x_{i}-S)^{2}}}$$
上記の「わかりやすいモデル」では、それぞれの誤差をフルスケールの±10%としたので、標準偏差RMSは、
$$RMS=フルスケール\times0.1$$
と、解釈できそうです。フルスケールを100L/minにしたので、流量計の読み値は、真値±10L/minずれるし、アナログ入力カードも真値±10L/minずれるという事ですね。
2乗和平方根(SRSS)
2乗和平方根が総合誤差の計算方法で、一番有力だと思います。 下記サイトでも2乗和平方根が使われています。標準偏差の累積に使われているようです。
nを誤差要因になる機器の数、xiを標準偏差とすると下記の式になります。
$$SRSS=\sqrt{\sum_{i=1}^{n}{x_{i}^{2}}}$$
つまり、上記の「わかりやすいモデル」で考えると、
$$SRSS=フルスケール\times\sqrt{(0.1)^{2}+(0.1)^{2}}$$
となり、総合誤差14%ぐらいで、読み値が真値±14L/minぐらい68%の確率でズレるということです。
もし、この試運転を行うとしたら、「実際に流している流量」、つまり「試運転用に用意した高精度で信頼できる流量計を同配管上に設置した流量」もしくは、「想定ではこのぐらい流れているはずの流量」と読み値が、「±15L/min以内に収まればよし。」という風に決めていきます。
実際のモデル
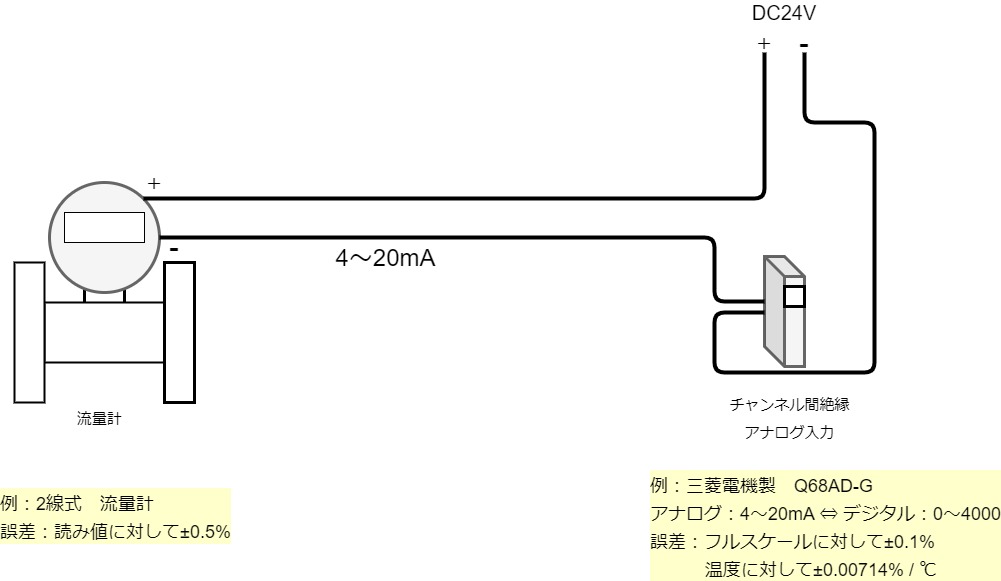
誤差は、読み値に対してだったり、フルスケールに対してだったりするので、気を付けましょう。アナログ入力カードには、温度が変化したときの誤差が書いてあったりしますが、これも総合誤差をだすときには、大抵は無視して考えます。試運転するときに流量を変えて許容誤差を見る事はありますが、温度を変えて許容誤差をみることは少ないからです。もし、密度を測定するときに温度による誤差も気にするなら、2乗和平方根で総合誤差を計算します。
実際には、読み値の誤差、フルスケールの誤差などすべて一緒にして二乗和平方根で総合誤差をだします。その値から安全を見て、ちょっと多めに許容できる誤差を設定します。


コメント